Abaixo vou deixar nossa ferramenta que gera um triângulo de pascal, basta você informar até que número deseja gerar e pronto.
Distância (em cm):
Ao utilizar os modernos conceitos matemáticos, muitas vezes pensamos que eles surgiram de intuições naturais dos grandes pensadores. Mas na verdade, o processo de construção das ferramentas que temos hoje levou séculos para se completar. Uma delas é triângulo de Pascal, que nos ajuda a resolver problemas binomiais e estatísticos, além de auxiliar a computação.
Neste artigo, explicaremos o que é o triângulo de Pascal, como ele funciona e quais são suas utilidades para os problemas matemáticos modernos.
O que é o triângulo de Pascal?
Antes de tratar dos conceitos mais específicos, vamos explicar o que é o triângulo.
O triângulo de pascal pode ser entendido como uma estrutura aritmética triangular infinita na qual a composição de cada integrante é realizada através de coeficientes binomiais que se inter-relacionam de diversas maneiras e possuem várias propriedades em comum.
Por ser infinito, o triângulo é montado de cima para baixo, começando no número 1 e prosseguindo de acordo com as regras de cada nível dos coeficientes.
O Coeficiente Binomial
Os componentes do triângulo de Pascal são conhecidos como números binomiais ou então, coeficientes binomiais. A estrutura de um número binominal pode ser representada por:
Sendo que n e p são números naturais e, necessariamente, n ≥ p. Nesta relação, o número n será conhecido como numerador e o número p, como denominador.
Para transformar o binômio é relação aritmética, podemos usar a representação:
Em que:
- Cn,p é a combinação simples de n elementos dados entre p a p
- n! é o fatorial de n, o qual pode ser calculado por: n.(n – 1).(n – 2)…3.2.1
- p!: fatorial de p, o qual pode ser calculado por: p.(p – 1).(p – 2)…3.2.1
Desta forma é possível obter o valor de qualquer coeficiente dados os elementos n e o intervalo p a p. Estes serão usados na montagem do triângulo.
Como surgiu o triângulo de Pascal
Os estudiosos afirmam que o triângulo de Pascal como representação geométrica foi estudado pela primeira vês na China imperial pelo matemático Yang Hui (1238-1298), enquanto a Europa vivia a idade média. Estudos também afirmam que outros matemáticos da época já delineavam teoremas envolvendo o triângulo.
Contudo, a partir do início da era moderna, com o italiano Niccolò Fontana Tartaglia (1499-1559) e o famoso matemático francês Blaise Pascal (1623-1662), que o triângulo chegou à forma e às funções que conhecemos hoje. Aliás, o nome do triângulo de Pascal é dado em homenagem ao célebre físico e matemático francês.
Foi Pascal quem descobriu a maior parte das propriedades do triângulo que conhecemos hoje. Ele sistematizou seu funcionamento e possibilitou que novas aplicações fossem feitas com a ferramenta, especialmente no campo da estatística, uma vez que os primeiros matemáticos o usavam basicamente para o cálculo de raízes.
Outra questão interessante, que foi descoberta posteriormente, é que os binômios de Newton e as sequências de Fibonacci podem ser encontrados a partir dos números que compõem o triângulo.
Como construir o triângulo de Pascal
A regra básica para a construção do triângulo de Pascal é que os números binomiais de mesmo numerador devem ser postos na mesma linha e os números binomiais de denominador, devem ser postos na mesma coluna.
Para exemplificar, vamos montar as 7 linhas iniciais do triângulo a seguir:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Quando expomos a forma gráfica, fica muito mais simples o entendimento do conceito do triângulo. Veja que na 2ª linha é composta de 1 e 1 porque o número 1 é o único número da linha anterior. Já a 3ª linha é composta por 1, 2 e 1, uma vez que 2 é a soma de 1 + 1, resultados da linha anterior.
Para entender perfeitamente, basca calcular a fórmula dos binômios usando a equação com fatoriais dada anteriormente.
As propriedades do triângulo de Pascal
Uma vez entendidos os conceitos por trás do triângulo de Pascal, vamos estudar algumas de suas propriedades:
- Todas as linhas do triângulo, necessariamente, começarão e terminarão com o número 1. É simples entender o porquê de isso acontecer. O primeiro elemento será calculado pela seguinte expressão:
E o último elemento será calculado pela seguinte expressão:
Sendo assim, todo primeiro e último números de cada linha serão iguais a 1.
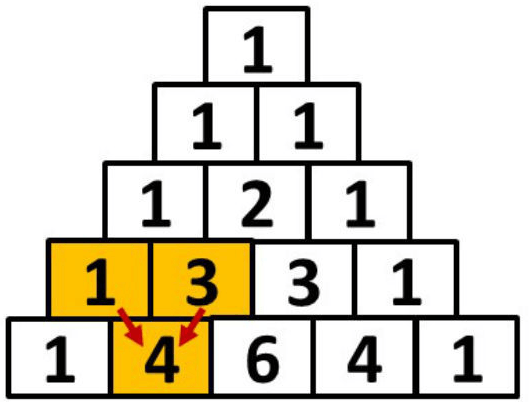
- Os demais número da linha (do 2º ao antepenúltimo) serão formados pela soma dos dois números mais próximos a eles na linha superior. Podemos entender isso pela Relação de Stifel, dada abaixo:
Veja como é fácil perceber no exemplo dado no tópico anterior, que o primeiro e o último números são iguais a 1 e que os demais são formados pela soma dos números imediatamente acima deles. Esta é a forma mais simples de se entender a formação do triângulo de Pascal.
Apenas para fins de esclarecimento, apresentamos abaixo mais uma imagem que demonstra a relação entre os números da linha superior com a formação de cada número das linhas inferiores.
- Os números equidistantes numa mesma linha, são exatamente iguais. Esta relação é muitos simples de ser entendida, veja no exemplo acima. Na 2º linha temos 1 e 1, na 3ª 1,2 e 1, na 4ª 1, 3, 3, 1 e assim sucessivamente.
A utilização no binômio de Newton
O binômio de Newton é uma potência no formato (x+y)n, em que x e y são números reais e que n é um número natural (1, 2, 3…).
Quando os valores de n são pequenos, a simples multiplicação dos fatores pode resolver o cálculo. Contudo, quando os valores de n são muito grandes, é necessário fazer o uso do triângulo de Pascal para expansão dos resultados e cálculo do valor final na expressão. A representação do binômio de Newton para montagem no triângulo de Pascal será dada por:
Conclusão
O triângulo de Pascal é extremamente útil para os modernos cálculos matemáticos. Especialmente os que trabalham com grande volume de dados, como as expressões fatoradas na forma de binômios de Newton com expoente de 3ª, 4ª, 5ª potências e etc.
O entendimento do triângulo e de suas propriedades pode ser de grande valia para estudantes, pesquisadores e profissionais de diversas áreas do conhecimento.

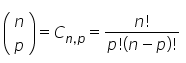
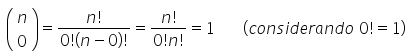
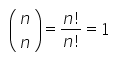
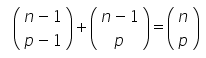
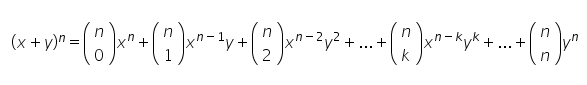
Gostaria do envio , em Números Primos , de 1.000.000 , 10.000.000 , 100.000.000 e 1.000.000.000 Dígitos Decimais para joriocarlossousamonteiro1965@gmail.com .