Calculadora de Proporção Online

Nesta página, você poderá facilmente calcular relações proporcionais entre diferentes quantidades. A calculadora foi projetada para ajudá-lo a resolver problemas de regra de três simples e compostos, permitindo encontrar valores desconhecidos com base em relações preestabelecidas.

Basta inserir os valores conhecidos nos campos apropriados e, em um clique, obter o resultado da proporção desejada. Nossa ferramenta torna a matemática simples e eficiente, proporcionando respostas precisas em questão de segundos. Experimente agora mesmo e simplifique seus cálculos de proporção!

O cálculo de proporção é uma técnica matemática usada para comparar quantidades e determinar a relação entre elas. Geralmente, é utilizado para encontrar valores desconhecidos com base em valores conhecidos e sua relação proporcional.

A proporção é uma comparação entre duas quantidades usando uma fração. A relação entre as duas quantidades é expressa como uma proporção, onde o numerador representa a primeira quantidade e o denominador representa a segunda quantidade. A proporção é escrita na forma “a:b” ou “a/b”, onde “a” e “b” são os valores comparados.

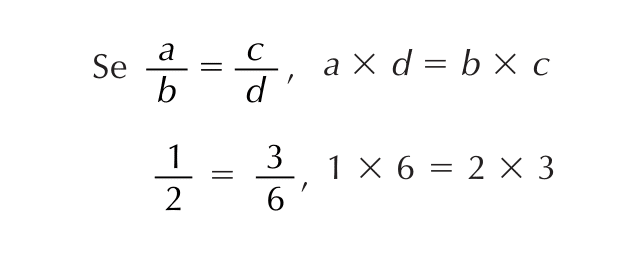
Existem diferentes tipos de proporção, incluindo:

1. Regra de Três Simples: É usado para encontrar um valor desconhecido com base em três valores conhecidos, onde dois valores estão em uma relação direta e o terceiro valor está na mesma proporção.
2. Regra de Três Composta: É usado quando mais de duas quantidades estão relacionadas. Envolve uma cadeia de proporções diretas ou inversas para encontrar o valor desconhecido.
3. Proporção Direta: Duas quantidades variam na mesma direção. Quando uma aumenta, a outra também aumenta, e quando uma diminui, a outra também diminui.
4. Proporção Inversa: Duas quantidades variam em direções opostas. Quando uma aumenta, a outra diminui, e vice-versa.

O cálculo de proporção pode ser aplicado em várias situações do dia a dia, como em problemas de matemática, regras de três comerciais, problemas de escala, cálculo de porcentagens, e muito mais.

Para ilustrar com um exemplo simples, vamos utilizar a Regra de Três Simples:

Exemplo: Se 4 litros de suco requerem 3 laranjas, quantas laranjas são necessárias para fazer 10 litros de suco?

Vamos usar a Regra de Três Simples para resolver o problema:

4 litros de suco -> 3 laranjas
10 litros de suco -> x laranjas

A proporção será: 4/3 = 10/x

Para encontrar o valor de x (laranjas), podemos fazer uma regra de três cruzada: 4x = 3 * 10 4x = 30 x = 30 / 4 x = 7.5

Portanto, são necessárias 7.5 laranjas para fazer 10 litros de suco.

Grandezas Diretamente Proporcionais:

Grandezas diretamente proporcionais são duas ou mais quantidades que variam na mesma direção. Isso significa que quando uma das grandezas aumenta, a outra também aumenta, e quando uma diminui, a outra também diminui, mantendo uma relação constante entre elas. Na forma matemática, isso é expresso como:

Se duas grandezas “a” e “b” são diretamente proporcionais, temos: a ∝ b

Ou seja, quando “a” aumenta em um certo fator, “b” também aumenta no mesmo fator, e vice-versa.

Exemplos de Grandezas Diretamente Proporcionais:

1. Velocidade e Distância: Quando um veículo viaja a uma velocidade constante, a distância percorrida é diretamente proporcional ao tempo. Se a velocidade aumenta, a distância percorrida em um período de tempo aumenta proporcionalmente.
2. Horas Trabalhadas e Salário: Em muitos trabalhos por hora, o salário de um funcionário é diretamente proporcional ao número de horas trabalhadas. Quanto mais horas forem trabalhadas, maior será o salário.
3. Quantidade de Material e Custo: Em alguns processos de produção, o custo total de um produto é diretamente proporcional à quantidade de material utilizado. Quanto mais material for usado, maior será o custo do produto final.

Grandezas Inversamente Proporcionais:

Grandezas inversamente proporcionais são duas ou mais quantidades que variam em direções opostas. Isso significa que quando uma das grandezas aumenta, a outra diminui, mantendo uma relação constante entre elas. Na forma matemática, isso é expresso como:

Se duas grandezas “a” e “b” são inversamente proporcionais, temos: a ∝ 1/b

Ou seja, quando “a” aumenta em um certo fator, “b” diminui no mesmo fator, e vice-versa.

Exemplos de Grandezas Inversamente Proporcionais:

1. Tempo e Velocidade: A distância percorrida por um veículo é inversamente proporcional à velocidade. Se a velocidade do veículo aumenta, o tempo necessário para percorrer a mesma distância diminui.
2. Intensidade da Luz e Distância: A intensidade da luz de uma fonte luminosa é inversamente proporcional à distância da fonte. Quanto mais distante a fonte luminosa, menos intensa será a luz que alcança uma superfície específica.
3. Pressão e Volume: A pressão de um gás é inversamente proporcional ao seu volume, desde que a temperatura e a quantidade de gás sejam mantidas constantes. Se o volume de um gás aumenta, a pressão diminui, e vice-versa. Esse é o princípio da Lei de Boyle, que descreve o comportamento de gases ideais.