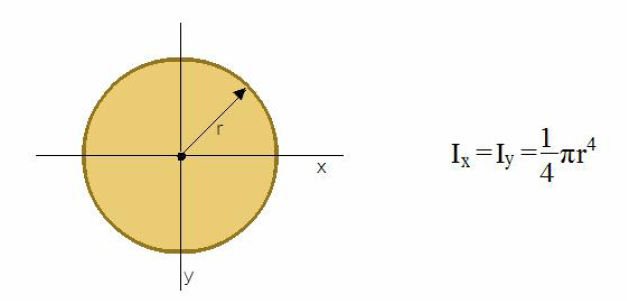Momento de Inércia Círculo (calculadora online)

Criamos uma calculadora bem simples para calcular o momento de inércia do circulo, você precisa apenas informar o valor do RAIO e clicar em calcular.

 

 

É muito importante termos um exemplo para entendermos a passagem de uma soma para um integral. Definir o momento de inércia, definir o momento angular, e nada melhor que termos um exemplo prático de como isso funciona. Neste artigo, vamos abordar o momento de inércia do círculo de uma forma literal. Continue lendo este artigo e compreenda mais sobre o momento de inércia do círculo.

• Arco Seno
• Arco Cosseno
• Área do Cone
• Arco Tangente
• Perímetro de um Circulo
• Área do Circulo
• Área da Esfera
• Área do Cilindro
• Volume da Esfera
• Volume do Cilindro
• Volume do Cubo

 

Momento de inércia do círculo

Vamos imaginar um círculo que podemos enxergá-lo de cima. Ou seja, de um ponto de vista como se ele estivesse feito em uma folha de papel. Imagine que este círculo que possui o raio “R”, não considerando a sua espessura, vamos imaginar somente à circunferência.

Agora, vamos imaginar que este círculo esteja em rotação em torno de um eixo perpendicular à sua superfície. Então, com a velocidade angular é “ômega”, e vamos  imaginar esse círculo sendo visto de lado. Desta forma, podemos designar a velocidade ômega como: W x K. Neste momento, ômega tornou-se a componente “z” da velocidade angular.

Após a interpretação acima, vamos determinar com base nestas circunstâncias, qual será o momento angular do círculo. O momento angular do círculo é uma soma sobre certos elementos infinitesimais. Neste caso, podemos ver este elemento como o iésimo pedacinho da circunferência do círculo, um pedaço muito pequeno da circunferência (anel). Esse pequeno pedacinho do círculo possui massa “dmi”, caracterizado por um vetor posição, chamado de “ri”. O ri é o iésimo pedacinho da circunferência do círculo que possui velocidade “vi”.

Então, dli = dmi x ri x vi

 

Temos duas alternativas para expressarmos “ri”. Podemos adotar a fórmula que utilizamos muitas vezes, onde escrevemos ri = R (raio, módulo de ri) x versor e com índice Rô (letra grega). Esse é um vetor que aponta na direção perpendicular à circunferência. Nessas circunstâncias, também sabemos que “vi” é a velocidade desse elemento de massa dmi, com velocidade = R x W (ômega) x o versor índice Phi (letra grega).

Tudo isso também pode ser escrito como ômega vetor ri, sendo escrito como W x ri, e como sabemos que ômega está na direção e no sentido do vetor K, então temos o vetor K e o índice Rô = índice Phi. Neste caso, escrevemos a expressão para ômega vetor ri. Neste caso, dl = dmi x R x RW, como o produto vetorial de Rô, índice Rô e índice Phi. O vetor índice Fi é um versor tangencial à circunferência. Por esse ponto, podemos ver que o índice Rô com o produto vetorial com índice Phi, é um versor perpendicular ao plano do versor “K”.

Bom, resumindo, podemos concluir que o eixo principal do círculo quando observamos ele com vista lateral, é o momento principal de inércia do círculo. Isso acontece porque a velocidade angular é um tipo de velocidade que somente possui a componente z, e o tensor de inércia nessas circunstâncias, tem elementos de matriz. A velocidade angular só tem a componente z, e portanto, “ômega”. É claro que vamos buscar encontrar apenas “Lz” diferente de zero e Lz = Izz x ômega.