Com apenas alguns cliques, você poderá obter rapidamente a área dessa forma geométrica tridimensional. Basta inserir o valor do raio da esfera e selecionar a unidade de medida desejada.
Nossa calculadora fará todos os cálculos necessários e apresentará o resultado de forma clara e precisa. Não importa se você está estudando matemática ou precisa calcular áreas em projetos do mundo real, nossa calculadora está aqui para ajudar.
Experimente agora mesmo e simplifique seus cálculos de áreas de esferas de maneira eficiente e conveniente.
*Instruções: Você precisa escolher a unidade de medida e depois informar o valor do Raio da esfera e clique em “CALCULAR”.
Ao observarmos o mundo ao nosso redor, podemos perceber que existe uma grande diversidade de figuras geométricas. São figuras que compõem detalhes de nosso cotidiano que muitas vezes passam despercebidas. O design e as combinações geométricas são ricas e estão presentes nas ciências, nas artes, na engenharia, etc. Dentre essas importantes figuras do nosso dia a dia, vamos falar sobre a esfera.
Neste artigo, vamos falar como é feito o cálculo da esfera com precisão e de forma simples, sem complicações. Acompanhe este artigo até o final e aprenda sobre este importante cálculo fundamental em diversa aplicações.

Definição de esfera
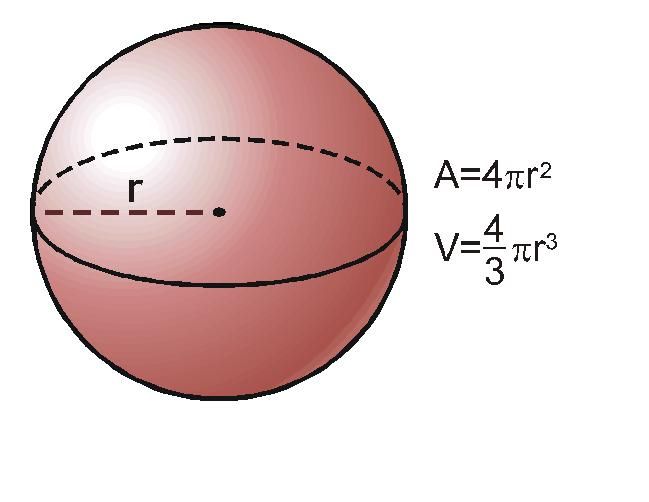
A esfera é um sólido geométrico com medida relacionada diretamente com sua superfície. Ou seja, sua semicircunferência pode estabelecer a área e o volume total. Por ser um sólido geométrico proveniente da disposição giro sobre um eixo, esse sólido apresenta um diâmetro (linha reta) que passa pelo centro de giro, interligando duas extremidades opostas.
Da mesma forma que é possível encontrarmos a área de qualquer outro objeto geométrico, também podemos obter a área da superfície de uma esfera. Essa medida é relacionada com a “casca” (medida da superfície da esfera). Através da fórmula utilizada para este fim, podemos encontrar a área total da superfície de uma esfera. Fazendo uso deste importantíssimo cálculo, as ciências e tecnologias modernas conseguem encontrar o fuso esférico e determinar coordenadas com precisão.
- Leia também sobre:
- Área do Circulo
- Área do Cone
- Calcular Área do Cilindro
Cálculo da área da esfera
Ao fazermos uso da fórmula A = 4πr2, conseguimos determinar a área de uma esfera. “A” representa a área da esfera e “r” representa o raio desta esfera. O Pi é uma constante da matemática, equivalente a 3,14.
Vamos a um exemplo prático:
Um renomado artista plástico pretende utilizar em uma de suas obras uma bola de isopor que ficará na parte superior desta arte. Porém, ele irá fazer a pintura desta esfera de isopor na cor preta. Nós sabemos que o raio desta esfera mede 1 m e que o m² da tinta que será utilizada custa R$ 150,00. Encontre o valor em R$ que será necessário para pintar essa esfera.
Solução:
Neste caso, devemos calcular a área referente a esfera de isopor e multiplicar esse valor de forma a monetizar os custos exatos com a tinta. Vamos encontrar o valor desta tinta por m²:
A = 4πr²
A = 4·3,14·1²
A = 12,56·1
A = 12,56 m²
Então, o artista plástico irá gastar exatamente R$ 1.884,00 para pintar a esfera com a tinta preta.
Definição de fuso esférico
Os importantíssimos fusos esféricos são parcelas de mesma medida de uma superfície esférica. Ao encontrarmos os fusos esféricos, também podemos encontrar os polos. Desta forma, através da regra de três é possível obter o valor da área do fuso esférico.
Devemos considerar “α” como o ângulo do fuso esférico e “Af” como a área do fuso. Assim, temos Af que pode ser utilizado como uma regra de três:
A = 360
Af α
Em seguida devemos multiplicar cruzado e obter:
A·α = Af·360
Af = A·α
360
A fórmula da área do fuso fica então da seguinte forma:
Af = A·α
360
Af = 4πr2·α
360
Af = πr²·α
90
Mas também pode ser utilizada a seguinte expressão:
Af = 2r²α
Vamos a um exemplo prático:
Encontre a área referente ao fuso esférico com um ângulo de 30° e com um raio de 2 metros.
Af = πr²·α
90
Af = 3,14·2²·30
90
Af = 3,14·4·30
90
Af = 376,8
90
Af = 4,19