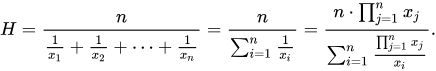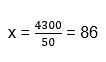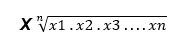Calculadora de Média Ponderada Online: aprenda a calcular

Com a ajuda da nossa administradora Yohana Pinto, responsável por todas as nossas calculadoras de estatísticas, conseguimos criar um sistema usando JS e HTML para fazer nossa calculadora de média ponderada online.

Recentemente recebemos um e-mail pedindo para criar uma calculadora de média aritmética ponderada, pensando em atender esta necessidade, criamos o sistema abaixo, você precisa inserir os dados pedidos e calcular.

É muito importante que você observe o exercício para que não ocorra nenhum erro no cálculo, confira todos os número da questão e separe-os em PESO e DADOS, isso irá organizar o seu problema.

• Calculadora de Média Aritmética Simples Online
• Calculadora de Média, Mediana e Moda Online
• Calculadora de Média Harmônica Online
• Média Geométrica (calculadora online)

 A matemática é um mundo fascinante e com possibilidades exatas de soluções para um problema. A partir dela, o Universo pode ser dimensionado de todas as formas possíveis. Conhecer um pouco sobre as possibilidades diante dos métodos e cálculos elaborados pelas mentes mais célebres neste assunto ao longo da história, é algo que todos deveriam buscar conhecer mais a fundo.

Afinal, a matemática está em tudo ao nosso redor. É através dela que podemos mensurar quantias e valores de tudo em nosso dia a dia. Sem ela, outras ciências nem existiriam. Os cálculos e métodos aplicados em diversas indústrias, engenharias e até na música, possibilitaram que grandes obras surgissem ao longo dos últimos milênios. Mas e você, sabe o básico de matemática? Sabe o que significa uma média ponderada?

Neste artigo, vamos falar mais sobre matemática e sobre tópicos importantes deste Universo de conhecimento. Hoje, vamos falar sobre média ponderada e outros tipos de médias utilizadas na matemática. Continue lendo este artigo até o final e saiba mais sobre os tipos de médias existente na matemática e como calcular média ponderada.

Média Aritmética

Uma média aritmética é o tipo de média mais conhecida e utilizada na matemática. Ela é de fácil assimilação e pode ser utilizada sem dificuldades por todos. Geralmente, ela é muito utilizada em sala de aula quando os alunos começam a estudar os diferentes tipos de médias utilizadas na matemática.

Um exemplo de média aritmética muito utilizado por professores em sala de aula, é mostrar para os alunos como calcular a média aritmética das notas finais. Para utilizar média aritmética, é necessário que existam um conjunto de dados para podermos criar uma estimativa em relação a esses dados. A média aritmética pode ser vista como a base para que as outras médias possam ser compreendidas e estudadas.

Da média aritmética, derivam dois tipos de médias, as médias simples e ponderada. A partir dessas duas médias, é possível obter cálculos simples e mais complexos na busca por uma média equivalente em um conjunto de dados.

Média aritmética simples

O modelo de média aritmética simples pode ser utilizado a partir da divisão da soma entre todos os valores pela quantidade de valores obtidos. Ou seja, trata-se de realizar a soma de todos os dados onde queremos estabelecer uma média e dividir o resultado obtido pela quantidade de dados existentes.

Para fazer isso, existe um símbolo expresso X. Vamos imaginar que uma quantidade “n” de dados diante de uma questão: (x1, x2, x3, …, xn), então, a média entre esses dados será:

X = x1+x2+x3+…+xn

n

Exemplo Prático

Um aluno finalizou o semestre com as seguintes notas: 9.1, 9.3, 8.1. Qual é a média aritmética simples das três notas obtidas?

Começamos por somar as três notas:

9,1 + 9,3 + 8,1 = 26,5

Em seguida, devemos dividir a quantidade de notas por 3:

26,5 / 3 = 8,8

Então, a média aritmética simples das notas obtidas pelo aluno do exemplo é de 8,8 pontos.

Exemplo Prático

Imaginamos uma turma com 20 alunos e outra turma com 30 alunos, as notas geradas pelas duas turmas nas atividades em sala de aula foram as seguintes notas respectivas:

• Turma da Manhã = 62, 67, 71, 74, 76, 77, 78, 79, 79, 80, 80, 81, 81, 82, 83, 84, 86, 89, 93 e 98.
• Turma da Tarde = 81, 82, 83, 84, 85, 86, 87, 87, 88, 88, 89, 89, 89, 90, 90, 90, 90, 91, 91, 91, 92, 92, 93, 93, 94, 95, 96, 97, 98 e 99.

Considerando a média aritmética simples da turma que estuda de manhã é de 80 e a média da turma da tarde é de 90. Mas, essa média não reflete a realidade de uma média única entre todos os alunos dos dois períodos. Neste caso, devemos calcular a média aritmética de todos os alunos:

Então, podemos ver que a média obtida das notas de todos os alunos foi de 86 pontos.

Média aritmética ponderada

A média aritmética ponderada traz mais um tipo de dado que deve ser incluído, o “peso” de cada item. Neste caso, podemos dizer que em um conjunto de dados onde iremos obter uma média, os itens são considerados de forma individual. Vamos imaginar que temos um conjunto de dados, com n quantidade: (x1, x2, x3, …, xn), e cada um desses dados recebe um peso: (p1, p2, p3,… pn) lançados de forma respectiva.

P  = x1p1 + x2p2 + x3p3 +… + xnpn

P1 + p2 + p3 +… + pn

Exemplo Prático

Um aluno realizou uma prova e conseguiu a nota 9.1, e obteve em um trabalho em sala de aula a nota 8.7. Considerando que o peso estipulado para a prova é 6 e para o trabalho em sala de aula é 4, qual é a média ponderada das notas desse aluno?

Começamos multiplicando 9,1 x 6 e somamos o resultado pela multiplicação de 8,7 x 4; então teremos 54,6 + 34,8 = 89,4. Em seguida, dividimos o resultado encontrado pela soma dos pesos: 6 + 4 = 10. O resultado final será 89,4 / 10 = 8,94. A média ponderada das notas da prova e do trabalho em sala de aula é de 8,94 pontos.

Além das duas médias que acabamos de mostrar, existem dois outros tipos de médias conhecidas no âmbito escolar:

Média geométrica

A média geométrica existente entre o conjunto de dados, traz “n” quantidades onde a média é obtida através da raiz de n. Considerando um conjunto de dados (x1, x2, x3, …, xn), a média geométrica entre todos esses dados será de:

Um bom exemplo do que estamos falando é a obtenção da média geométrica entre 2, 8 e 32. Vamos obter a média geométrica desses números:

Começamos analisando que temos três dados para podermos traçar uma média geométrica comum entre eles.

Então, podemos ver que a média geométrica entre os dados 2, 8 e 32 será 8.

Média harmônica

A média harmônica é um recurso de medida de médias onde podemos obter a média de “n” dados. Levando em conta um conjunto de n dados (x1, x2, x3, …, xn), podemos estabelecer uma média harmônica entre os dados indicados da seguinte forma: