Calcular Perímetro de um Circulo (calculadora online)

Entender sobre as figuras geométricas é uma coisa muito importante desde sempre, principalmente para cálculos matemáticos. A geometria plana é muito explorada por engenheiros, matemáticos, artistas, dentre outras profissões. Ao nos aprofundarmos diante dos cálculos envolvendo figuras geométricas planas, acabamos nos deparando com o perímetro.

Neste artigo iremos falar sobre o cálculo do perímetro em um círculo e ensinar de forma simples e sem complicações a encontrar esta medida. Continue lendo o artigo até o final e aprenda a calcular o perímetro de um círculo.

 

 

 

Perímetro ou Circunferência

A medida estabelecida como perímetro de uma figura geométrica é calculada levando em conta o comprimento dos lados desta figura. A somatória desses comprimentos irá resultar no perímetro da figura em questão. Sendo assim, não temos nenhuma expressão pré-definida enquanto a isso.

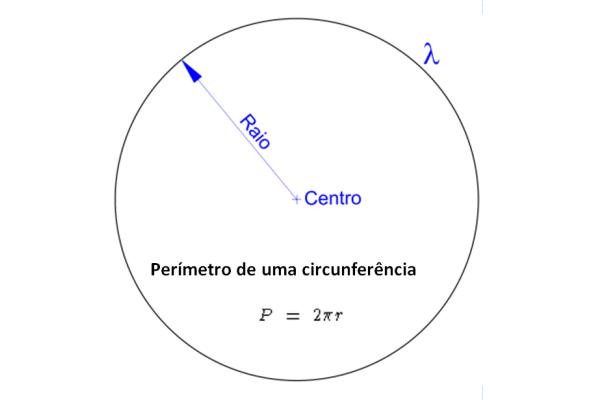
Na circunferência, a maneira como se deve calcular o perímetro é diferente, sendo que as figuras circulares não possuem segmento de reta. Ou seja, sua borda é circular, e para determinarmos o perímetro de um círculo devemos considerar outros elementos. Um desses elementos é o raio (r), levando em conta seu comprimento e sabendo que quanto maior esta medida maior será a circunferência deste círculo.

• Veja outras calculadoras:
• Área do Circulo
• Área do Cone
• Área da Esfera
• Calcular Área do Cilindro

Então, para que possamos determinar de forma simples e sem complicações a circunferência, ou melhor dizendo, o perímetro de um círculo, devemos fazer uso de uma única expressão. Devemos observar com atenção sempre o tamanho do raio e levar isto em conta:

C = 2 x π x r, sendo que:

C = Perímetro ou Comprimento da circunferência

π = 3,14

r = raio da circunferência

Vamos a um exemplo prático da aplicação do perímetro de um círculo:

 

Exemplo 1:

Determine a quantidade de metros que uma pessoa irá percorrer se der 8 voltas em torno de um círculo de 2 metros de raio referente a um canteiro central de uma praça.

 

Solução:

C = 2 x π x r

C = 2 x 3,14 x 2

C = 12,56

Distância percorrida

C = 12,56 x 8

C = 100,48 metros

Então, podemos dizer que esta pessoa percorreu um distância de 100,48 metros.

 

Exemplo 2:

A medida de um pneu possui um raio de 400 mm, quantos metros são percorridos quando esse pneu dá uma volta completa?

 

Solução:

Devemos transformar 400 mm em metros, e para fazer isso, vamos dividir 400 por 1.000, obtendo como resultado 0,4 m. Desta forma, devemos aplicar a expressão que nos dará a circunferência de um círculo.

C = 2 x π x r

C = 2 x 3,14 x 0,4

C = 2,512 metros

Então, sabemos que a cada volta deste pneu são percorridos 2,5 metros.

 

Exemplo 3

Um ciclista profissional irá percorrer uma distância de 600 km em uma prova. Essa distância será percorrida em uma pista circular que possui um raio de 100 m. Quantas voltas esse ciclista irá percorrer nesta prova?

 

Solução:

Circunferência da pista:

C = 2 x π x r

C = 2 x 3,14 x 100

C = 628 metros

Então, sabemos que o ciclista irá percorrer uma distância de 628 metros a cada volta, agora, devemos saber quantas vezes essa medida cabe em 600 km. Realizando os cálculos, a conta segue da seguinte forma:

600.000/628 = 955

Então, o ciclista irá percorrer 955 voltas nesta prova.

Obs: o número 600.000 é referente aos 600 km da prova: 1.000 metros x 600 km = 600.000 metros.