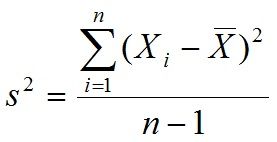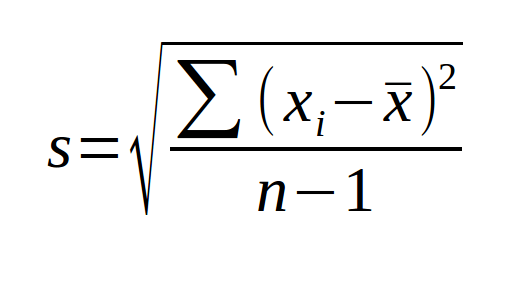Calculadora de Desvio Padrão Online

Bom, hoje nós apresentamos nossa mais nova ferramenta, a calculadora de desvio padrão, variância, média e erro padrão da média. Usar a ferramenta é muito fácil, você precisa apenas informar os valores separados por vírgula (exemplo: 10,43,87,12,2,4,78,90…). É muito importante que você informe dos dados corretamente para que não ocorra nenhum erro.

Abaixo da calculadora nós deixaremos algumas explicações e exemplos de desvio padrão para você entender mais sobre o assunto. Vou deixar também algumas videoaulas de professores para que não reste nenhuma dúvida.

Quando estamos falando de desvio padrão e variância estamos falando de medidas de dispersão. Esse sistema de medidas é eficiente para ajudar a identificar se um determinado conjunto de dados está regular. Essa indicação é feita com base na média aritmética tomada como ponto de partida para essa verificação.

Neste artigo, vamos falar sobre o desvio padrão e a variância mostrando para que esse cálculo serve e como ele é feito. Vamos mostrar um exemplo deste tipo de cálculo e como proceder com eles. Continue lendo este artigo até o final e saiba mais sobre o assunto e como calcular o desvio padrão e a variância.

Desvio Padrão e Variância

Quando estamos estudando Estatística, podemos contar com algumas estratégias eficientes quando vamos fazer a verificação dos valores apresentados em um determinado conjunto. Os dados de um conjunto podem ser dispersos, podendo estar distantes uns dos outros.

O tipo de ferramenta que é utilizada para empregar esse método são conhecidas como as médias de dispersão, onde são utilizadas a variância e o desvio padrão. Vamos ver em específico o que cada uma delas representa.

Variância

Diante de um determinado conjunto contendo dados, a medida de dispersão variância irá mostrar com eficiência a distância existente entre os valores em cada conjunto, mostrando a distância em que o conjunto se encontra com referência ao valor central.

Neste caso, quanto menor for a variância, mais próximo serão os valores relacionados a média. Porém, quanto maior for essa medida, maiores os valores estarão das médias. Vamos considerar x1, x2,…, xn, correspondendo a “n” elementos diante de uma amostra, sendo “x” a média aritmética de todos esses elementos. Neste caso, o cálculo da variância irá apontar os dados da seguinte forma:

Var. amostral = (x₁ – x)² + (x₂ – x)² + (x₃ – x)² + … + (x_n – x)²

                                                        ​n – 1

Em contrapartida, buscamos calcular a variância populacional, e para fazer isso, consideramos a quantidade total de elementos referente a população, e não focamos somente em uma amostra. Porém, neste caso, o cálculo será feito com uma pequena diferença em comparação com o cálculo anterior:

Var. populacional = (x1 – x)² + (x2 – x)² + (x3 – x)² + … + (xn – x)²

                                                            n

Desvio Padrão

Já no caso do desvio padrão, podemos identificar onde existe um erro na amostragem de dados. Ou seja, o conjunto poderá ser verificado no intuito de encontrar uma discordância nos dados e assim poder substituí-los pela média aritmética do conjunto. O desvio padrão poderá ser observado na média aritmética que também irá informar o quanto ela é confiável na demonstração deste valor. Você poderá encontrar os valores dispostos da seguinte forma: média aritmética (x) ± desvio padrão (dp)

Esse cálculo é feito a partir de raiz quadrada positiva relacionada com a variância. Então, podemos utilizar a seguinte fórmula: dp = √var

Quando aplicamos o cálculo da variância junto ao cálculo do desvio padrão, conseguimos elaborar as medidas de dispersão de um conjunto.

Exemplo Prático

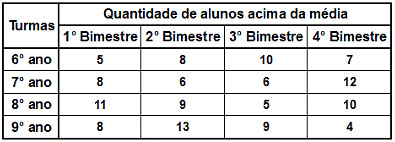
Em uma escola, os coordenadores decidiram realizar a observação da quantidade de alunos que atingiram notas acima da média em todas as matérias avaliadas. Para que essa informação fosse melhor observada, a diretora da escola resolveu montar um tabela com a quantidade de notas azuis em um conjunto de dados de quatro turmas no período de um ano. Observe abaixo como ficou a tabela elaborada pela diretora da escola:

Antes de ser realizado o cálculo da variância, se fez necessário uma verificação da média aritmética (x) referente a quantidade existente de alunos que estavam acima da média nas turmas analisadas:

6° ano → x = 5 + 8 + 10 + 7 = 30 = 7,50.

4               4

7° ano → x = 8 + 6 + 6 + 12 = 32 = 8,00.

4               4

8° ano → x = 11 + 9 + 5 + 10 = 35 = 8,75.

4              4

9° ano → x = 8 + 13 + 9 + 4 = 34 = 8,50.

4                     4

Para fazer o cálculo da variância referente a quantidade de alunos que se encontravam acima da média nas turmas avaliadas, o cálculo necessitou de uma amostragem. Devido a isso, foi necessário a utilização da fórmula da variância amostral seguida do seguinte cálculo:

Var. amostral = (x1 – x)² + (x2 – x)² + (x3 – x)² + … + (xn – x)²

n – 1

6° ano → Var = (5 – 7,50)² + (8 – 7,50)² + (10 – 7,50)² + (7 – 7,50)²

4 – 1

Var = (– 2,50)² + (0,50)² + (2,50)² + (– 0,50)²

3

Var = 6,25 + 0,25 + 6,25 + 0,25

3

Var = 13,00

3

Var = 4,33

7° ano → Var = (8 – 8,00)² + (6 – 8,00)² + (6 – 8,00)² + (12 – 8,00)²

4 – 1

Var = (0,00)² + (– 2,00)² + (– 2,00)² + (4,00)²

3

Var = 0,00 + 4,00 + 4,00 + 16,00

3

Var = 24,00

3

Var = 8,00

8° ano → Var = (11 – 8,75)² + (9 – 8,75)² + (5 – 8,75)² + (10 – 8,75)²

4 – 1

Var = (2,25)² + (0,25)² + (– 3,75)² + (1,25)²

3

Var = 5,06 + 0,06 + 14,06 + 1,56

3

Var = 20,74

3

Var = 6,91

9° ano → Var = (8 – 8,50)² + (13 – 8,50)² + (9 – 8,50)² + (4 – 8,50)²

4 – 1

Var = (– 0,50)² + (4,50)² + (0,50)² + (– 4,50)²

3

Var = 0,25 + 20,25 + 0,25 + 20,25

3

Var = 41,00

3

Assim que é conhecida a variância de uma turma, podemos realizar o cálculo do desvio padrão:

6° ano

dp = √var

dp = √4,33

​dp ≈ 2,08

7° ano

dp = √var

dp = √8,00

​dp ≈ 2,83

8° ano

dp = √var

dp = √6,91

​dp ≈ 2,63

9° ano

dp = √var

dp = √13,66

​dp ≈ 3,70

Var = 13,66

Então, para concluirmos o nosso exemplo de como calcular desvio padrão e variância da quantidade de alunos com notas acima da média, ficamos com as notas acima da média nas seguintes turmas:

6° ano: 7,50 ± 2,08 alunos com notas acima da média por bimestre;

7° ano: 8,00 ± 2,83 alunos com notas acima da média por bimestre;

8° ano: 8,75 ± 2,63 alunos com notas acima da média por bimestre;

9° ano: 8,50 ± 3,70 alunos com notas acima da média por bimestre.