Calculadora de Média, Mediana e Moda Online

Para facilitar a sua vida, criamos uma calculadora online de moda, média e mediana. Você precisa apenas informar os números do conjunto e clicar em calcular. Lembre-se que você precisa informar os números separados por vírgula.

 

Os cálculos estatísticos são baseados em diversos parâmetros como média, moda e mediana. Esses itens muito utilizados determinam valores com base em um grupo de elementos, podendo ser números, características, eventos, entre outras aspectos de análise. Por serem muito utilizados, esses parâmetros possuem resolução bastante simples e fácil de ser aplicada até mesmo no dia a dia.

Neste post, falaremos o que é média, moda e mediana, considerando alguns exemplos e as principais características de cada uma dessas modalidades. Além disso, ensinaremos a seguir como calcular média, moda e mediana através de alguns exemplos simples e fáceis. Confira tudo isso a seguir e muito mais.

 

O que é média, moda e mediana?

Cada uma dessas palavras indicam um tipo de cálculo diferente para obter valores estatísticos sobre uma determinada análise. Todos esses cálculos correspondem a análises de grupos definidos por meio de pesquisas. Alguns desses índices é bastante fácil de entender, como a média, que corresponde sempre ao valor médio de determinada análise. No entanto, a seguir falaremos um pouco sobre cada um desses parâmetros considerando suas características.

• Potência com Expoente Negativo
• Potência com Expoente Fracionário
• Desvio Padrão e Variância
• Calcular Coeficiente de Variação
• Triângulo de Pascal
• Média Geométrica

 

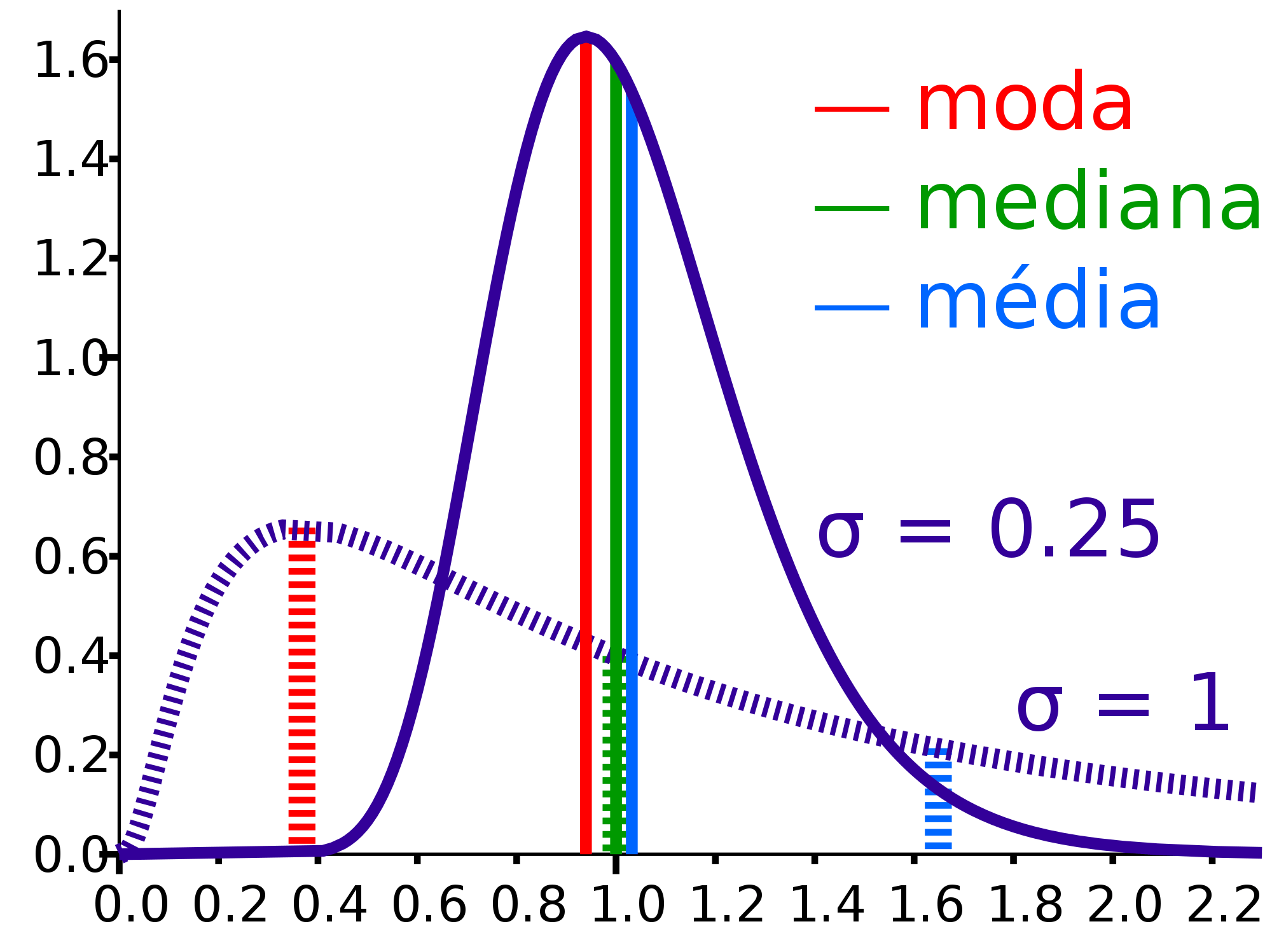
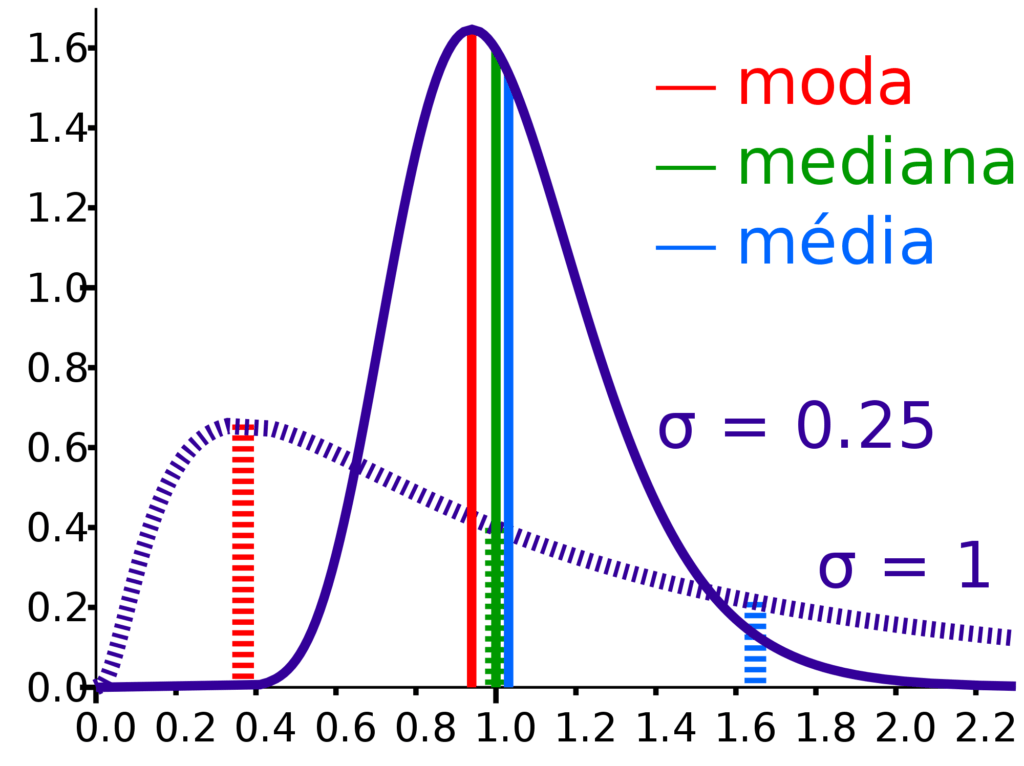
Média

A média é dada pela soma de todos os números dividida pelo número que corresponde a todos os elementos. Com esse cálculo, é possível obter uma média de todos os resultados agrupados, onde o valor médio pode ser descrito em decimal ou em porcentagem.

 

Moda

Como o próprio nome já diz, a moda é realmente aquilo que mais aparece em um grupo. Por exemplo, quando dizemos que determinada roupa está na moda, é porque todo mundo está comprando está roupa e por isso ela aparece no guarda-roupa da maioria das pessoas. Isso também é aplicado na análise estatística. Nesse caso, os dados que mais aparecem em um determinado grupo são o resultado do cálculo da moda.

 

Mediana

Já a mediana é sempre o valor ou elemento que aparece exatamente no meio de todo a sequência do grupo. Por exemplo, em uma sequência numérica de 1 a 9, a mediana é o número 5, pois ele é o número que aparece exatamente no meio dessa sequência. Lembrando que ao avaliar a mediana é importante colocar os números ou elementos em uma sequência respeitando a ordem crescente de cada um.

 

Como calcular média, moda e mediana?

Agora que você já sabe o conceito de média, moda e mediana, podemos seguir para as fórmulas de cálculo ou análise de cada um desses parâmetros estatísticos. Nesse caso, vamos aos exemplos e aplicações de cada cálculo de forma separada. Confira os cálculos a seguir:

 

Cálculo da média

Para calcular a média, devemos sempre lembrar que a fórmula é bastante simples e utiliza apenas soma e divisão. Nesse caso, a fórmula é descrita da seguinte forma: média = soma dos valores / número de valores. Aplicando essa fórmula é possível obter o resultado de qualquer grupo numérico. Vamos a um exemplo prático para você entender melhor como funciona essa relação de média:

 

Exemplo 1

A professora de uma determinada turma do ensino médio quer saber a média das notas alcançadas por seus alunos. Calcule a média das notas dessa turma considerando os dados a seguir:

8,5

9

6

3

7

8

2

5

7

8

9

5

Média = (8,5 + 9 + 6 + 3 + 7 + 8 + 2 + 5 + 7 + 8 + 9 + 5) / 12

Média = 77,5 / 12

Média = 6,5

Nesse primeiro exemplo, temos 12 notas diferentes que corresponde a 12 alunos do ensino médio. A soma de todas essas notas resultaram no número 77,5, que por sua vez foi dividido pelo total de notas, que é 12. O resultado disso tudo foi a média de 6,5. Isso significa que a média de notas alcançada pelos alunos dessa professora foi de 6,5.

 

Exemplo 2

O dono de um restaurante deseja saber a média de vendas de um suco de laranja por dia. Para saber essa média, o dono do restaurante elaborou uma planilha com as informações de vendas dentro do período de uma semana. Calcule a média de vendas por dia com base na tabela a seguir:

16

30

25

47

23

15

26

Média = (16 + 30 + 25 + 47 + 23 + 15 + 26) / 7

Média = 182 / 7

Média = 26

Considerando o cálculo acima, temos que as vendas diárias foram somadas em um período de 7 dias, onde o resultado foi dividido pelo total de dias de análise. Nesse caso, a média de sucos vendidas por dia com base na análise de uma semana é de 26.

 

Cálculo da moda

O cálculo da moda é ainda mais fácil do que da média. Nesse caso, não existe uma fórmula nem mesmo um indicador complexo para obter o resultado da moda. Tudo que precisamos fazer é observar qual número ou elemento aparece mais vezes dentro do grupo analisado. Sendo assim, vamos aos exemplos:

 

Exemplo prático

A gerente de uma biblioteca comprou 10 exemplares de livros, onde cada título corresponde aos números ordinais (1º, 2º, 3º e 4º). No entanto, alguns títulos vieram repetidos, e a intenção da gerente é identificar quais são os títulos que mais se repetem. Calcule a moda com base nos dados a seguir:

1º

3º

4º

2º

2º

4º

1º

1º

3º

1º

Moda = elemento com maior número de repetições

1º = 4

2º = 2

3º = 2

4º = 2

Moda = 1º (com 4 repetições)

Considerando os dados acima, temos que todos os títulos se repetem dentro do grupo de 10 títulos comprados pela gerente da biblioteca. No entanto, o título 1º é o que mais possui número de repetições, sendo um total de 4 repetições. Nesse caso, a moda é justamente o título 1º.

 

Cálculo da mediana

Para calcular a mediana de um determinado conjunto numérico ou de elementos, é necessário apenas colocá-los em ordem crescente e determinar o valor que aparece no meio de todo esse conjunto. Confira como fazer isso no exemplo a seguir:

 

Exemplo prático

Uma empresa recebeu 11 currículos para uma determinada vaga de emprego. Dentre esses currículos, as idades variaram de 18 a 45 anos. Calcule a mediana das idades com base na tabela a seguir:

38

45

18

23

25

24

23

26

18

31

42

Mediana = 18 | 18 | 23 | 23 | 24 | 25 | 26 | 31 | 38 | 42 | 45

Mediana = 25

Considerando os dados acima, temos que a mediana é o valor que aparece no meio da sequência numérica em ordem crescente. Nesse caso, o resultado é o número 25.