Após assistirmos o vídeo do canal Pô bichô Matemática, nossos desenvolvedores conseguiram criar uma calculadora para calcular a área do pentágono totalmente online.
Você só precisa fornecer alguns valores importantes e sempre ficar atento a unidade de medida de todos os elementos. Vale lembrar que o perímetro de um pentágono regular é 5 vezes o seu lado (L). Fique atento ao enunciado da sua questão.
*Instruções: Você precisa apenas informar o valor do Lado, da apótema, escolher a unidade de medida e clicar em “CALCULAR”.
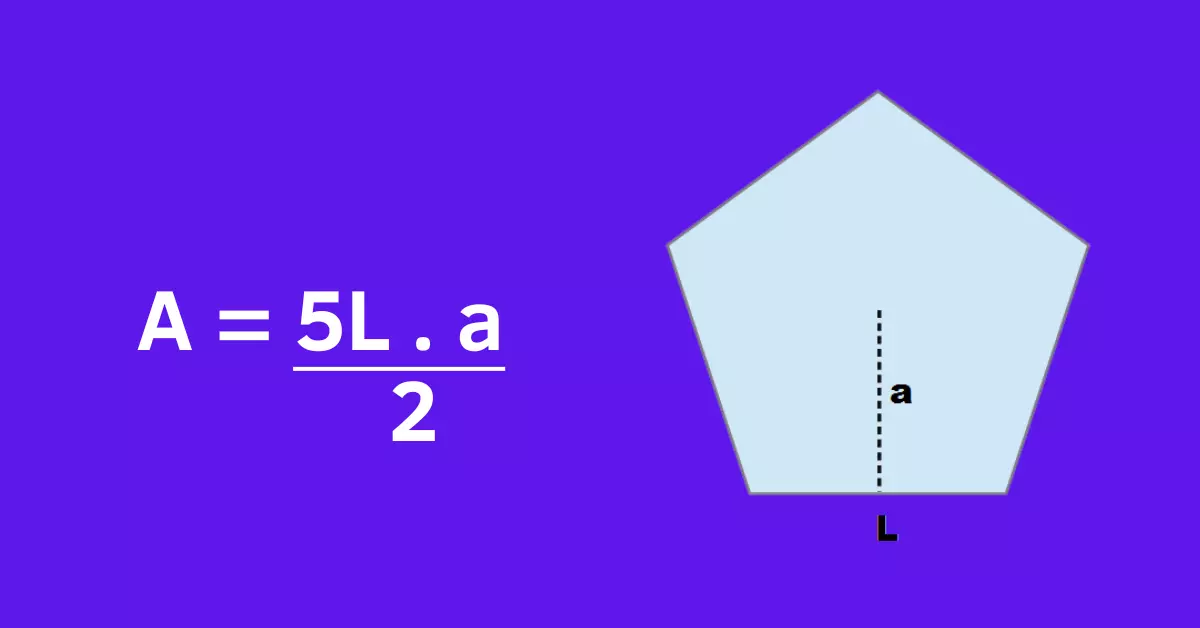
Veja duas formas diferentes de encontrar a área do pentágono
O pentágono pode ser visto como um polígono de cinco lados retos presente em grande escala no cotidiano das pessoas. A indústria mecânica utiliza esse polígono em peças que constitui máquinas e ferramentas. Na maioria dos casos, são utilizados pentágono regular, muito explorado nos exercícios e enunciados.
Neste artigo vamos mostrar como é calculado a área do pentágono sem mistérios e complicações. A área de um pentágono pode ser encontrada através de maneiras diferentes. Acompanhe este artigo até o final e aprenda de forma simples o cálculo da área do pentágono.
Encontrando a área do pentágono a partir do comprimento lateral e do apótema
Primeiramente, você deverá aplicar esse método em pentágonos regulares, possuidores de cinco lados iguais. Deverá levar em conta o comprimento lateral e a medida do apótema do pentágono. O apótema é um linha que parte do centro do pentágono e vai até o seu lado, formando um ângulo de 90° e um triângulo reto.
É importante que você não confunda apótema com a medida do raio (r), que é a linha que estabelece contato com o vértice (canto). O apótema irá tocar o ponto central exato do lado interno de um pentágono. A partir do comprimento do lado e do raio, você deverá seguir a leitura do próximo método. Vamos utilizar um pentágono medindo comprimento de 3 unidades e o apótema com medida igual a 2 unidades.
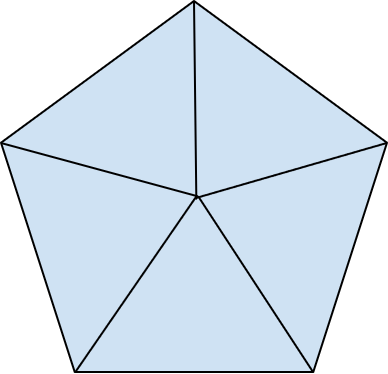
Em seguida, divida esse pentágono em cinco triângulos. Você deverá desenhar cinco linhas que irão começar no centro do pentágono indo até cada um dos cantos (vértices) do pentágono. Desta forma você irá obter cinco triângulos.
Agora calcule a área de cada triângulo de medida igual a base de cada lado. A altura desses triângulos possuem as mesmas medidas do apótema. Para se calcular a área de um triângulo basta que você utilize ½ x base x altura. Irá ficar da seguinte forma:
½ x 3 x 2 = 3 unidades.
A = A x 5
= 3 x 5
= 15
A = 3
Encontrando a área do pentágono a partir do comprimento lateral
Você deverá começar utilizando o comprimento do lado do pentágono. Essa metodologia irá funcionar somente com pentágonos regulares, possuidores de cinco lados iguais. Vamos tomar como exemplo um pentágono com lado igual a 7 unidades.
Você deverá dividir esse pentágono em cinco triângulos iguais. Faça o desenho de uma linha que irá partir do centro do pentágono e estar ligada a um dos pontos vértices. Faça isso em todos os pontos e você terá os cinco triângulos, como na figura acima no começo do artigo.
Você deverá dividir o triângulo por sua metade. Faça um desenho que vai do centro do pentágono até a base dos triângulos. Será uma linha que tocará a base dispondo de um ângulo reto de 90°, e faça a divisão dos triângulos por dois triângulos menores.
Você deverá rotular um dos triângulos menores. Nesta etapa, já podemos rotular um dos lados dos triângulos menores com um pequeno ângulo, esse ângulo será de 36°.
Calcule a altura deste triângulo. A altura deste triângulo será equivalente a sua linha de ângulo reto, que parte do centro de qualquer um dos lados deste pentágono. Trata-se de um triângulo tangente.
tan 36° = oposto/adjacente
O exemplo que estamos utilizando possui 3,5/altura
Altura x tan 36° = 3,5
Altura = 3,5/tan 36°
Altura = 4,8 unidades
Agora calcule a área do triângulo. A área deste triângulo será igual a ½ x altura (A = 1/2bh). Insira o valor da altura na fórmula do triângulo pequeno. No exemplo dado, a área do triângulo menor é de: ½ bh = 1/2(3,5)(4,8) = 8,4 unidades quadradas.
Faça a multiplicação para descobrir a área do pentágono. Um desses triângulos menores irá cobrir 1/10 relativo a área no pentágono. Para se chegar a área total, faça a multiplicação da área do triângulo menor por 10. Então, o resultado da área do pentágono será 8,4 x 10 = 84 unidades quadradas.
Veja também...
Adriano Silva
Formado em Técnico em Eletrônica, programador amador, especialista em SEO e apaixonado pelo gerenciamento de conteúdo digital.