Calculadora de Área do Cilindro

Com uma interface amigável e simples de usar, a nossa calculadora é ideal para estudantes, professores, engenheiros, arquitetos, e qualquer pessoa que precise realizar o cálculo da área do cilindro. Experimente agora mesmo a nossa calculadora online e agilize seus projetos e trabalhos!

Diante do grande quadro de figuras geométricas que podemos encontrar em nosso cotidiano, o cilindro é uma das que mais irão aparecer no dia a dia das pessoas. Assim como o círculo, o quadrado, a esfera, o trapézio, e muitas outras figuras importantes, o cilindro também aparece. Muito utilizado pela indústria e por formar componentes mecânicos essenciais, está figura geométrica é muito explorada.

Em vista disso, iremos falar sobre o cilindro e como é realizado o cálculo da área de sua área. Vamos mostrar através de exemplos práticos como é realizado o cálculo da área total  de um cilindro da forma mais simples possível. Continue lendo este artigo até o final e tire suas dúvidas do que é um cilindro e como é calculado sua área.

Definição de Cilindro

O cilindro pode ser visto como um sólido geométrico com muitas aplicações nos diversos tipos de indústria. Essa figura geométrica é considerada um corpo redondo por possuir uma de suas faces com formato arredondado. Devido a essa importante característica, o cálculo da área total de um cilindro irá precisar de mais observações e de um certo cuidado.

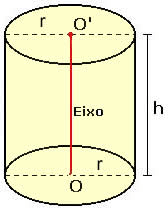
Vamos considerar um cilindro circular reto com um raio (r) da base e a altura (h), como é possível observarmos na figura abaixo:

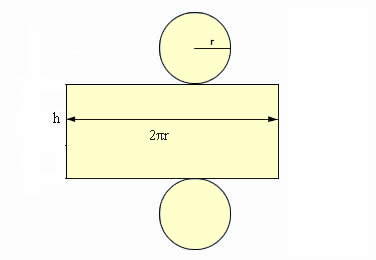
Para podermos entender melhor como é feito o cálculo da área de um cilindro, devemos fazer a planificação desta figura.

Observe que quando fazemos a planificação do cilindro nós obtemos duas circunferências com raios relativos à medida das bases. As medidas apresentadas neste tipo de sólido é igual a um retângulo com altura (h) e comprimento 2πr. Então nós podemos concluir que:

A área total é igual a área lateral somada a área da base duas vezes. Como a base de um cilindro são duas circunferências, então temos a seguinte fórmula:

• Área da base =  π∙r2
• Área lateral = 2∙π∙r∙h

Desta forma, nós podemos então determinar que a área total de um cilindro pode ser da seguinte forma:

• St = 2∙π∙r∙h + 2∙π∙r2

Quando colocamos 2πr em destaque, podemos observar que: St = 2∙π∙r∙(h + r)

Sendo essa a fórmula para o cálculo total deste sólido geométrico, que necessita dos seguintes dados:

St = é a área total de um cilindro

r = é o raio da base de um cilindro

h = é a altura relativo a um cilindro

Então, para podermos fazer o cálculo da área de um cilindro, devemos conhecer as medidas da altura e do raio.

Vamos aos exemplos práticos:

Exemplo 1:

Vamos determinar a área total de um cilindro com 16 cm de altura e com a medida do raio relativo a base de 5 cm. Utilize (π = 3,14).

Dados:

h = 16 cm

r = 5 cm

St = ?

Ao fazermos uso da fórmula da área total, podemos verificar que:

St = 2∙π∙r∙(h+r)

St = 2 ∙ 3,14 ∙ 5 ∙(16 + 5)

St = 2 ∙ 3,14 ∙ 5 ∙ 21

St = 659,4 cm²

Então, vimos que a área total desse cilindro é de 659,4 cm²

Exemplo 2:

Uma indústria planeja realizar a produção de um tonel de formato cilíndrico para armazenar óleo. O raio da base deste barril é de 40 cm e sua altura é de 1,2 m. Para realizar a produção do barril serão utilizadas chapas de material metálico. Qual será a medida necessária em m² deste material metálico para a fabricação de um barril?. Utilize  π = 3,14.

Dados:

h = 1,2 m

r = 40 cm = 0,4 m

St = ?

Através da fórmula total da área podemos obter:

St = 2∙π∙r∙(h + r)

St = 2 ∙ 3,14 ∙ 0,4 ∙ (1,2 + 0,4)

St = 2 ∙ 3,14 ∙ 0,4 ∙ 1,6

St = 4,02 m²

Então, serão utilizados 4,02 metros quadrados do material metálico escolhido para confeccionar cada barril.