Olá a todos, hoje apresentamos a todos vocês nossa calculadora de potência com expoente em fração. Seguindo o mesmo caminha da calculadora de potência com expoente negativo, você precisa informar se o número base será inteiro ou fração, depois precisa informar o número base, o expoente em forma de fração (exemplo: 6/7, utilize barra / ) e clique em calcular.
Abaixo da calculadora eu vou deixar algumas explicações com exercícios resolvidos e também algumas vídeo-aulas encontradas no YouTube. Veja o artigo até o fim para você ficar por dentro da matéria.
OBS.: os resultados apresentados em nossa calculadora são apresentados com números inteiros, as respostas em provas são geralmente apresentadas em forma de RAIZ, por isso a importância de ler o artigo até o fim.
Ao estudarmos as potências e suas aplicações, nos deparamos com diversas propriedades ligadas aos expoentes. Na matemática, um determinado número com um expoente, é dito como um um número elevado. Quando esse número é racional e calculado em unidades, elevar tal número a um expoente “x” não é dificultoso, mas e quanto devemos elevar um número a um expoente fracionário, como devemos proceder neste caso?
Neste artigo, vamos ensinar a calcular uma potência com expoente fracionário através de conteúdo explicativo e exemplo prático. Continue lendo este artigo até o final e saiba mais sobre esse assunto e como calcular potência com expoente fracionário.
Expoente fracionário: como calcular?
Quando estudamos as potências e as propriedades derivadas deste Universo de propriedades, podemos especificar diversos pontos. Hoje, vamos especificar os expoentes fracionários e compreendermos qual é o verdadeiro significado destes expoentes. Quando um expoente é escrito em forma de fração, o que devemos fazer?
Para compreendermos e saber de fato como calcular os expoentes fracionários, vamos partir de um número qualquer:
Neste caso, podemos fazer a escrita deste número no formato de uma raiz quadrada. Isso é possível de ser feito, pois o denominador da fração é 2, e o número irá ficar da seguinte forma:
Neste momento, é provável que você esteja se questionando, qual é a função do número 1 encontrado no numerador? Esse número faz parte do expoente do número (a). Porém, neste caso, não existe a necessidade de expressarmos esse número. Quando temos um número dentro de uma raiz, temos a possibilidade de fazermos todo o processo da forma inversa. Ou seja, podemos reescrever tal número como uma potência fracionária.
Devemos lembrar que quando escrevemos um número que traz uma potência fracionária, fazemos uso das seguintes propriedades:
- O numerador da potência está ligado ao expoente do número presente na base;
- O denominador da potência está ligado ao grau referente a raiz (no exemplo acima é uma raiz cúbica, com grau 3).
Para fazer a transformação de um número em uma raiz com potência fracionária, nos possibilita realizar a multiplicação do número da base, mas isso acontece com raízes de graus diferentes uns dos outros.
Exemplo Prático
Vamos transformar essas radiciações em números com potências fracionárias e logo em seguida vamos multiplicar esses números:
Em seguida, nós podemos fazer o cálculo da multiplicação dos números que dispõem da mesma base:
Então, caso queiramos fazer a escrita deste número no formato de radiciação, vamos ter o seguinte número:
Exemplo Prático
Também podemos simplificar uma potência com expoente fracionários com números elevados ao quadrado encontrados dentro da raiz. Neste caso, o numerador e o denominador são iguais, portanto:
Para finalizarmos, podemos fazer uma generalização da forma de transformação de uma potência com expoente fracionário para uma radiciação, também o inverso disso:
Exemplo Prático
Conclusão
Então, nós podemos definir que existe para expoentes fracionários com numeradores diferentes de 1.
Por exemplo, quando escrevermos como
, logo temos:
Podemos ver isso quando simplificamos levando ao cubo a raiz quadrada de 16. Essa mesma simplificação também pode ser realizada ao extrairmos a raiz quadrada do cubo de 16.

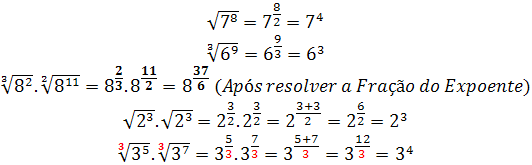
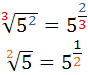
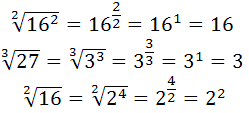
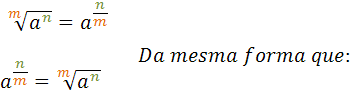
Você(s) é (são) incrível(incríveis) mesmo! Gostei imensamente da explicação e da ferramenta que disponibilizou/disponibilizaram. Parabéns e progresso!
gostei muito me ajudou e tanto