Momento de Inércia Retângulo (calculadora online)

Calculadora online para momento de inércia de um retângulo, essa é a nossa mais nova ferramenta. Essa nos deu muito trabalho, você precisa informar o valor do lado e da altura, lembre-se que precisa ser em Metros, caso não esteja, faça a conversão antes de calcular na ferramenta.

 

 

O momento de inércia é um tipo de grandeza física associada diretamente a inércia de rotação. Esse indicador da inércia aponta para a tendência que um determinado corpo massivo possui em se manter em movimento ou em seu estado inicial. Além disso, o cálculo também é aplicado a resistência que o corpo massivo pode ter para mudar o movimento de rotação. Todas essas características são aplicadas no cálculo do momento de inércia.

Neste post, falaremos o que é momento de inércia, quando esse cálculo é aplicado, qual é o conceito de inércia, entre outras informações importantes. Além disso, ensinaremos como calcular o momento de inércia de um retângulo. Confira tudo isso a seguir e muito mais.

 

O que é momento de inércia?

O momento de inércia é a distribuição da massa de um corpo partindo do centro de rotação. Isso quer dizer que a inércia é a tendência do corpo ficar parado ou entrar em movimento, dependendo dos aspectos aplicados a ele. Sendo assim, o momento de inércia é a dificuldade desse corpo massivo girar, independente do sentido que seja.

Por isso, sempre que falamos em momento de inércia há uma resolução de dois pontos em específicos, onde cada ponto corresponde a uma direção diferente. Nesse caso, é comumente utilizado o ponto y e o ponto x para determinar as duas direções que o corpo massivo pode se movimentar. Cada um desses pontos é ligado ao eixo central do corpo massivo, sendo assim, esse corpo pode girar tanto para a esquerda quanto para a direita.

Quando é questionado o momento de inércia de determinada figura, o que queremos saber é a dificuldade que esse corpo massivo tem para girar em seu próprio eixo, independente se ele irá girar para a direita ou para esquerda.

O momento de inércia é dado, no caso do retângulo, através das seguintes características de cálculo:

I = inércia;

b = base;

h = altura.

Nesse caso, a fórmula aplicada para o cálculo do momento de inércia do retângulo é constituído pelos seguintes aspectos: I = b . h³ / 12. Sendo assim, temos que a inércia é igual a base multiplicada pela altura ao cubo divididos pelo número 12. Essa fórmula é simétrica na vertical e na horizontal, por isso, é possível aplicar esse cálculo nas duas direções de rotação do retângulo.

Para calcular a inércia do retângulo, é necessário determinar os dois eixos, sendo eles y e x, e aplicar a fórmula anterior. Como já mencionamos, essa é a fórmula simplificada e simétrica, por isso, ela pode ser aplicada tanto na horizontal quanto na vertical, o que possibilita saber o momento de inércia dos dois lados de direção com uma única fórmula.

Se aplicarmos esse cálculo em um retângulo, obteremos o momento de inércia do corpo massivo retangular girar no sentido y e no sentido x. Nesse caso, falamos que o momento de inércia de cada lado se aplica a dificuldade que o corpo massivo de característica retangular terá para girar em cada um dos sentidos partindo de seu próprio eixo central.

 

Como calcular o momento de inércia do retângulo?

Considerando todos os itens mencionados anteriormente, temos a fórmula para o cálculo do momento de inércia e a resolução de cada um dos elementos desse cálculo. Como já mencionamos, o momento de inércia de um retângulo é calculado tanto na vertical quanto na horizontal. Isso porque essa figura apresenta dois sentidos de rotação, onde os sentidos são descritos pelas letras y e x.

Para calcular essa inércia, é necessário aplicar a fórmula (I = b . h³ / 12) nos dois sentidos de direção (y e x). Sendo assim, como resultado teremos o momento de inércia, ou a dificuldade, que o corpo massivo retangular possui em girar tanto para o sentido y quanto para o sentido x. Vamos a um exemplo prático de como calcular o momento de inércia de um retângulo:

 

Exemplo prático

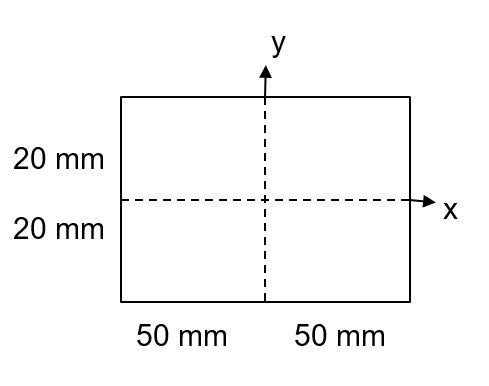
Veja a seguir o exemplo de um retângulo com todas as suas características necessárias para o cálculo da inércia do corpo massivo:

Agora, vamos obter o momento de inércia do sentido y e do sentido x a partir da fórmula já mencionada. Nesse caso, teremos as seguintes resoluções para o cálculo:

I(y) = 0,04, 0,1³ / 12

Resultado: 3,33 x 10⁻⁶ m⁴

Se analisarmos a figura acima, a base de cálculo para o sentido y são os 20 mm descritos entre o ponto A e C. Somando os dois números, temos o total de 40 mm. Por isso, a base utilizada para o cálculo do momento de inércia do sentido y é 40 mm, ou 0,04 m. Já a altura dessa figura é dada pelos valores opostos, ou seja, os 50 mm descritos na figura. Somando esses dois números, teremos 100 mm, que em metros fica 0,1.

O resultado dessa operação é o número 3,33 x 10⁻⁶ m⁴. Se observarmos, o resultado mostra a expressão em m⁴, que é causada pelo fato de usarmos a base e a altura em metros. Como a altura em cubo já aponta para o resultado em m³, e a base também está em metro, o resultado deve ser m⁴.

Agora, vamos fazer todo esse cálculo novamente para identificar a tendência que o corpo massivo retangular tem de girar para o eixo x. Nesse caso, teremos o seguinte cálculo:

Ix = 0,1 . 0,04³ / 12

Resultado: 5,33 x 10⁻⁷ m⁴

No cálculo da inércia de sentido x, a base para o cálculo passa a ser a soma dos 50 mm (100 mm), que é definida em 0,1 m. A altura do cálculo é dada pela soma dos 20 mm (40 mm), que é definida por 0,04 m. Tudo isso também é dividido pelo número 12.

Se observarmos os dois cálculos, o resultado da inércia de x é menor do que o resultado da inércia em y. Isso quer dizer que a análise do momento de inércia do retângulo do nosso exemplo aponta que a tendência desse corpo massivo rotacionar para o sentido y é muito maior do que para a rotação no sentido x. Sendo assim, podemos concluir que a maior tendência será sempre a que tiver um número menor, pois é mais difícil para o corpo massivo quebrar a inércia no sentido com maior número.