Abaixo deixo nossa calculadora para momento de inércia de um cilindro, é muito importante que você leia o artigo abaixo da ferramenta para que você entenda como funciona o cálculo.
Toda figura geométrica ou corpo massivo possui um eixo de rotação que é medido de acordo com a distribuição dessa massa em torno de todo o corpo. Quando esse eixo está em uma situação estável, isso significa que o corpo massivo está inerte ou parado. Mas quando é necessário rotacionar esse corpo para um dos lados, é aplicado o conceito de momento de inércia sobre a figura.
Neste post, ensinaremos o que é momento de inércia, considerando suas aplicações, conceitos e informações necessárias sobre essa grandeza. Além disso, mostraremos como calcular momento de inércia de um cilindro partindo de seu eixo central. Confira tudo isso a seguir e muito mais.
Momento de inércia
O momento de inércia pode ser representado como a dificuldade, facilidade ou tendência de um determinado corpo massivo rotacionar para um sentido em específico. Já a inércia é a situação onde esse mesmo corpo massivo se encontra parado, ou seja, ele não está rotacionando para nenhum dos lados. Quando é necessário rotacionar o corpo para algum dos lados, o momento de inércia é medido como a tendência maior dele rotacionar para determinado sentido ou dificuldade em fazer essa rotação.
Sendo assim, sempre que o assunto é momento de inércia é importante ter em mente que há dois sentidos de rotação, onde na maioria dos casos é expresso a partir do ponto y e do ponto x. Para melhor entendimento, você pode associar esses pontos a direita e esquerda partindo do ponto central da figura. Cada um desses pontos são tidos como eixos de movimento no cálculo de inércia, onde cada eixo é ligado ao eixo central da figura. Por isso, todo cálculo de momento de inércia precisa ter informações do eixo central do corpo massivo.
Quando há a necessidade de saber o momento de inércia de um corpo massivo, isso significa que é necessário saber para qual dos lados esse corpo massivo apresentará maior dificuldade em rotacionar. Quanto maior é o resultado do momento de inércia, mais dificultoso é essa rotação para o sentido avaliado. Isso porque com um número maior, é mais difícil quebrar essa inércia e assim rotacionar. Já no caso do resultado menor, isso significa que há uma maior tendência do corpo massivo rotacionar para aquele sentido, considerando que a inércia é quebrada mais facilmente.
Além de todas essas características, é importante ter em mente que nem todas as figuras e corpos massivos possuem uma distribuição de massa equivalente. No caso de um retângulo, por exemplo, a distribuição de massa ocorre de forma diferente, por isso, um dos sentidos apresentará maior facilidade para a rotação, enquanto o outro apresentará maior dificuldade em relação ao momento de inércia.
Já no caso de corpos massivos simétricos, como é o caso do círculo, a rotação igualmente entre os dois sentidos, por isso, o momento de inércia também é igual. A única diferença que pode ser observada nesse caso é em relação a distribuição da massa, que pode ser central ou nas extremidades da figura. Caso a massa seja mais concentrada ao centro do círculo, o momento de inércia se torna menor, ou seja, é muito mais fácil rotacionar para qualquer sentido. Mas caso a massa seja distribuída nas extremidades do círculo, a rotação se torna mais dificultosa para os dois sentidos de rotação.
Isso acontece porque a força exercida para sair do estado inerte é maior quando há mais concentração de massa nas extremidades. Quando a massa está concentrada no eixo central, o corpo massivo não exerce tanta força para rotacionar, tornando a rotação mais fácil e até mesmo mais ágil.
Aliás, isso também se aplica as figuras com distribuição de massa diferente, como acontece nas figuras como retângulo e triângulo. No caso do retângulo, o lado maior dessa figura apresenta mais massa que o lado menor, sendo assim, quando a rotação parte desse lado para qualquer sentido é mais difícil rotacionar o corpo massivo. Já no lado com menor concentração de massa, essa rotação se torna mais fácil para qualquer lado.
Como calcular momento de inércia do cilindro?
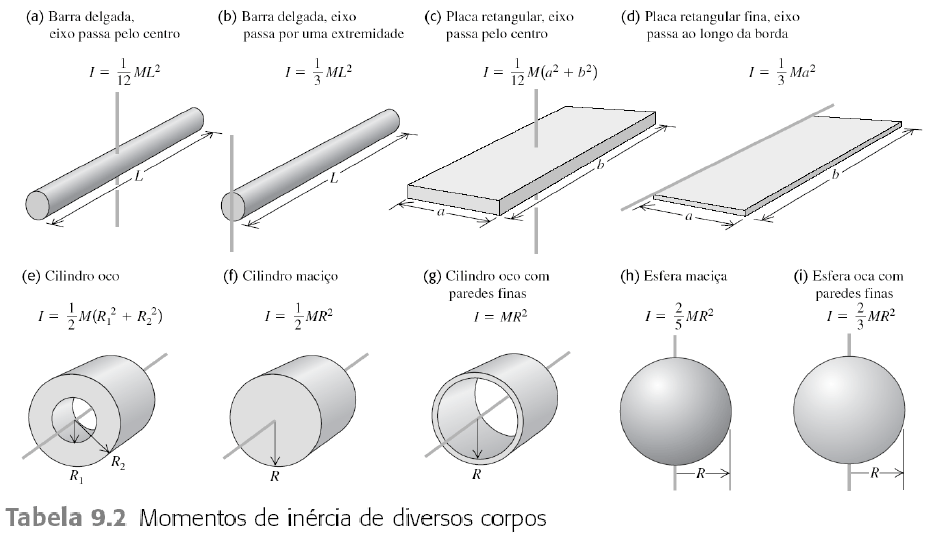
Em um cilindro uniforme, o momento de inércia é calculado partindo de seu eixo central, ou seja, o eixo que passa por dentro do cilindro. Para calcular esse momento de inércia é necessário aplicar a seguinte fórmula: I = 1/2 m R². Nesse caso, a resolução desses elementos é feita na seguinte forma:
I = momento de inércia;
R = raio dele mesmo;
r = raio de 0 a R;
Z = eixo central;
m = metro.
Agora, tudo que você precisará fazer para calcular o momento de inércia de um cilindro do tipo uniforme é substituir as informações descritas na fórmula desse cálculo. Lembrando que dependendo dos elementos é necessário realizar outros cálculos, como raio, comprimento e eixo. Além disso, fatores como a densidade do cilindro também são considerados para o cálculo dependendo das informações obtidas na questão a ser resolvida.
O cálculo do momento de inércia do cilindro ainda pode ser feito a partir de outra fórmula, onde é descrito as direções de rotação. Nesse caso, temos a seguinte fórmula: I (z) = mr² / 2, I (x) = I (y) = 1/12 m (3r² + h²). Considerando esta fórmula, temos as seguintes informações sobre o cálculo:
r = raio;
h = altura;
m = massa;
x e y = sentidos de direção;
z = eixo central.
Para calcular o momento de inércia do cilindro uniforme a partir dessa segunda fórmula é necessário apenas substituir cada uma das informações do cálculo pelos respectivos dados do cilindro. Além dessas fórmulas e expressões de cálculo, é importante saber que o momento de inércia de um cilindro uniforme para um cilindro com paredes espessas é diferente. Isso porque o raio central é medido em duas etapas, sendo elas: r1 (raio até a primeira parede do cilindro) e r2 (raio até a segunda parede do cilindro).
Sendo assim, é necessário utilizar outra fórmula específica para esse cálculo que irá considerar esses dois raios presentes no cilindro de paredes espessas. Em todos os casos e fórmulas, para calcular o momento de inércia desse corpo massivo é preciso substituir as informações e aplicar o cálculo de acordo com a ordem descrita nas fórmulas.