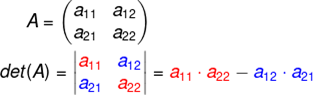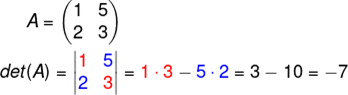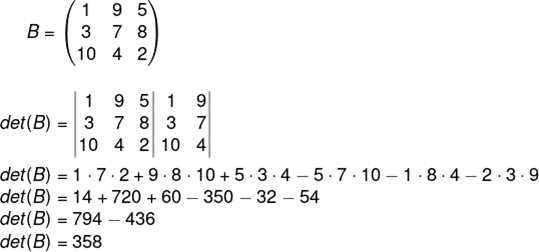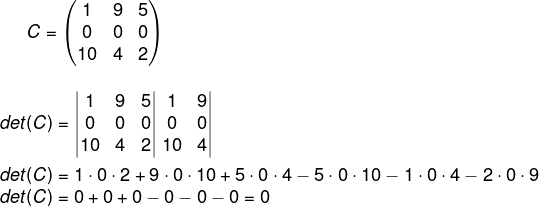Calculadora Determinante Matriz

Criamos nossa calculadora online de determinante de uma matriz. Você poderá escolher a ordem da matriz (2×2, 3×3, 4×4, 5×5 e por ai vai…). Siga as instruções para conseguir o melhor resultado.

 

Como calcular determinante de uma matriz?

Uma determinante é uma função matricial que junto de uma matriz quadrada se torna um escalar e saber como calcular determinante de uma matriz é essencial para identificar o escalar correto da sua operação. Por sua vez, a escalar determina como um número real que relacionado a uma matriz quadrada se torna um número único. Então para cada matriz quadrada de ordem sempre irá existir um número que será único relacionado a ela.

 

O que é uma matriz?

Na matemática uma matriz é uma tabela onde ficam linhas e colunas organizadas em um formato m x n sendo que “m” representa a numeração da linha e “n” representa a numeração da coluna. As linhas são em formato vertical e as colunas em formato horizontal, e elas possuem diversas aplicações sendo de extrema importância na matemática.

 

Como faz para calcular um determinante de uma matriz?

Utilizamos um determinante de uma matriz para calcular se 3 pontos estão alinhados no plano cartesiano, para realizar o cálculo de um triângulo para sistemas lineares e outras aplicações matemáticas. Estes estudos não se limitam à matemática, pois também fazem parte do estudo do campo elétrico com aplicações na física.

Só é possível calcular determinantes das matrizes quadradas quando a quantidade de linhas e colunas são iguais. Para calculá-las, precisamos primeiro determinar a sua ordem, como, por exemplo, 1×1, 2×2, 3×3, 4×4, etc.

*Vídeo feito por Brasil Escola

 

Veja a seguir como calcular o determinante de matriz de ordem 1:

Quando a matriz possui somente 1 linha e 1 coluna ela é conhecida como ordem 1, ou seja, possui somente 1 elemento. No caso, possui um único termo. Veja o exemplo prático a seguir:

A=(A₁₁)

det(A) = |2| = 2

Neste caso é necessário conhecer apenas um elemento.

Agora iremos mostrar como se calcula um determinante de matriz 2. Neste caso iremos ter produtos diferentes do termo diagonal principal e diagonal secundário. A seguir veremos um exemplo algébrico com construção de det(A):

 

Por exemplo:

 

Iremos ensinar sobre o determinante de ordem 3, mas para isso teremos primeiro que ensinar a regra de Sarrus.

A regra de Sarrus é uma forma de calcular determinante de matrizes de ordem 3, o que torna necessário seguir alguns passos.

O primeiro passo é duplicar as duas primeiras colunas no final da matriz, veja o exemplo:

O segundo passo é fazer a multiplicação dos termos de cada uma das três diagonais que se encontram no mesmo sentido:

A seguir veremos um exemplo de 3 determinante.

 

Primeira propriedade:

Se uma das linhas for igual a zero o determinante será igual a zero, por exemplo:

 

Segunda propriedade:

Se A e B forem duas matrizes det(AB) = det(A) · det(B), exemplo:

Veja como fica o cálculo dos determinantes separados:

det(A) = 2 · (-6) – 5 · 3

det(A) = -12 – 15 = -27

det(B) = 4 · 1 – 2 · (-2)

det(B) = 4 + 4 = +8

Então det(A) · det(B) = -27 · 8 =  -216

Existem outros exemplos de propriedades, mas aqui apresentamos dois para que você entenda como funciona esse cálculo.