Momento de Inércia Triângulo

Segue abaixo nossa calculadora para o momento de inércia de um triângulo, você precisa apenas informar a Base e a altura da figura. Vale lembrar que é muito importante que a medida esteja em metros, caso contrario, a ferramenta apresentará resultado incoerente.

 

A facilidade ou dificuldade de girar um corpo massivo para um determinado sentido é dado pela expressão “momento de inércia“. Essa importante grandeza física que está associada diretamente com a rotação de um corpo massivo, determina qual é o sentido de um corpo massivo e para que lado ele é capaz de girar com mais facilidade ou dificuldade, dependendo do resultado obtido no cálculo.

Neste post, falaremos em detalhes o que é momento de inércia, para que serve esse indicador, quais são as principais características do cálculo e aplicações práticas. Além disso, ensinaremos como calcular momento de inércia de um triângulo através de exemplos e fórmulas simples. Confira tudo isso a seguir e muito mais.

 

O que é e para que serve a inércia de uma figura?

O momento de inércia é ponto central de um corpo massivo onde a massa é distribuída igualmente. Essa distribuição faz com que a figura fique parada, ou inerte. O momento de inércia é exatamente a circunstância ou número que indica a facilidade ou a dificuldade que um determinado corpo massivo possui em girar para algum sentido. Por exemplo, considerando a direita e a esquerda de um retângulo, temos que um dos sentidos terá uma dificuldade maior para que o corpo se movimente, enquanto que o outro sentido terá uma dificuldade menor, ou mais facilidade.

Sendo assim, podemos concluir que o momento de inércia determina a dificuldade ou a facilidade de que uma figura rotacione em volta de seu próprio centro de massa ou eixo. Nesse caso, também podemos dizer que o momento de inércia é a tendência desse corpo massivo rotacionar para um determinado sentido avaliado no cálculo.

Independente da figura, haverá sempre dois sentidos para que o momento de inércia seja calculado. Esses sentidos podem ser expressos de várias formas, mas o mais comum é a utilização das letras y e x, onde cada letra parte do eixo central do corpo massivo. Nesse caso, o questionamento é feito da seguinte forma: qual é a tendência, momento de inércia, do corpo massivo girar para o sentido y e x?

Considerando esses dados, temos que o momento de inércia pode ser aplicado em diferentes figuras geométricas e objetos que apresentam corpo massivo. Dependendo do eixo pretendido, o cálculo é alterado, assim como as diferentes fórmulas utilizadas para descobrir a maior tendência do corpo massivo rotacionar para um dos lados.

 

Conceito e interpretação do momento de inércia

Para entender perfeitamente o que é momento de inércia, devemos associar que quanto maior é a massa distribuída pelo corpo massivo, maior é a dificuldade em rotacionar esse corpo. Isso significa que se a massa estiver mais concentrada ao centro do corpo massivo, mais fácil será rotacionar esse mesmo corpo.

No caso da inércia de uma figura geométrica que não possui distribuição simétrica, como é o caso do retângulo, triângulo, entre outras figuras geométricas com distribuições diferentes em vários sentidos, o momento de inércia para a rotação dos sentidos se diferencia justamente por causa dessa distribuição diferente. Por exemplo, o círculo possui distribuição simétrica, onde os dois sentidos y e x possuem a mesma inércia para rotação, ou seja, a dificuldade para rotacionar o círculo para o sentido y é a mesma observada na rotação no sentido x.

Já no caso do retângulo essa inércia varia, pois, cada um dos sentidos possui uma distribuição de massa diferente. O mesmo se aplica ao triângulo e a outras formas geométricas que não possuem distribuição simétrica entre todo o corpo massivo. Ainda sobre o círculo, se a massa é concentrada no centro do corpo massivo, a rotação se torna muito mais fácil. Mas se a massa está mais presente nas extremidades dessa figura, a rotação de se torna mais difícil.

Isso tudo ainda é associado a velocidade, força rotacional e outros cálculos aplicados na física. Quanto menor é a inércia de uma figura, ou seja, menor é a dificuldade do corpo massivo rotacionar para algum dos lados, maior é a velocidade alcançada.

 

Como calcular momento de inércia do triângulo?

Diferente das formas geométricas com distribuição de massa simétrica, o triângulo apresenta uma distribuição diferente entre os diferentes lados. Por isso, esse corpo massivo se enquadra no teorema dos eixos paralelos, o que significa que para calcular o momento de inércia de um triângulo é necessário identificar primeiro o eixo que torna o triângulo inerte. Nesse caso, é necessário descobrir o “centróide“, que é exatamente essa área do triângulo que o torna inerte a qualquer movimento. Sendo assim, vamos a fórmula do centróide do triângulo:

Considerando todos esses elementos de cálculo, temos a seguinte fórmula do centróide do triângulo: X = 0, Y = h/3, A = b * h /2.

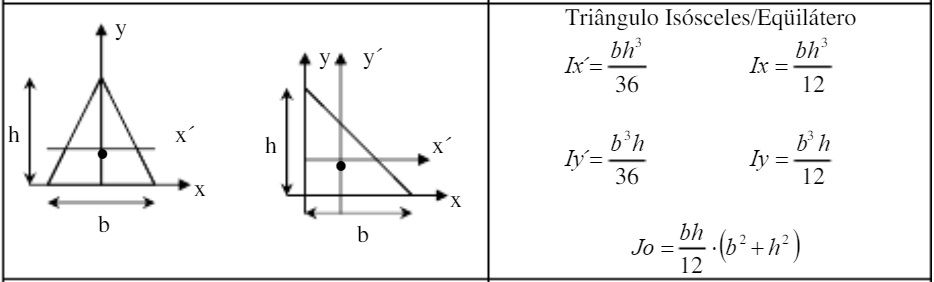
O resultado dessa fórmula é fundamental para calcular o momento de inércia do triângulo. Agora, se você já sabe qual é o centróide giratório, o cálculo da inércia do triângulo pode prosseguir com a seguinte fórmula: I (x cg) = bh³/36, W (x) = b.h²/12, I (x) = h. /6.

A resolução desses dados é feito da seguinte forma:

I = momento de inércia;

x = eixo rotacional ou direção;

cg = centróide giratório;

b = base;

h = altura.

Lembrando ainda que dependendo do tipo de triângulo o cálculo é feito com uma fórmula diferente. A fórmula mencionada tanto para o centróide giratório quanto para o momento de inércia correspondem ao triângulo do tipo isósceles ou equilátero. Se o triângulo for um triângulo retângulo, é necessário aplicar outras fórmulas diferentes que podem variar dependendo de várias características apresentada pela figura geométrica.

Para calcular o momento de inércia de um triângulo do tipo isósceles, é necessário obter o resultado do centróide giratório e depois aplicar a fórmula mencionada logo acima. Esse cálculo pode ser feito com qualquer triângulo desse tipo, desde que os dados sejam respeitados conforme foi descrito anteriormente.

Além disso, todos os elementos descritos na resolução do cálculo do momento de inércia do triângulo devem ser substituídos pelos valores que correspondem ao triângulo analisado. Sendo assim, para realizar o cálculo basta substituir as informações e calcular de acordo com a ordem de cada equação.